General Model Recommendations
Model
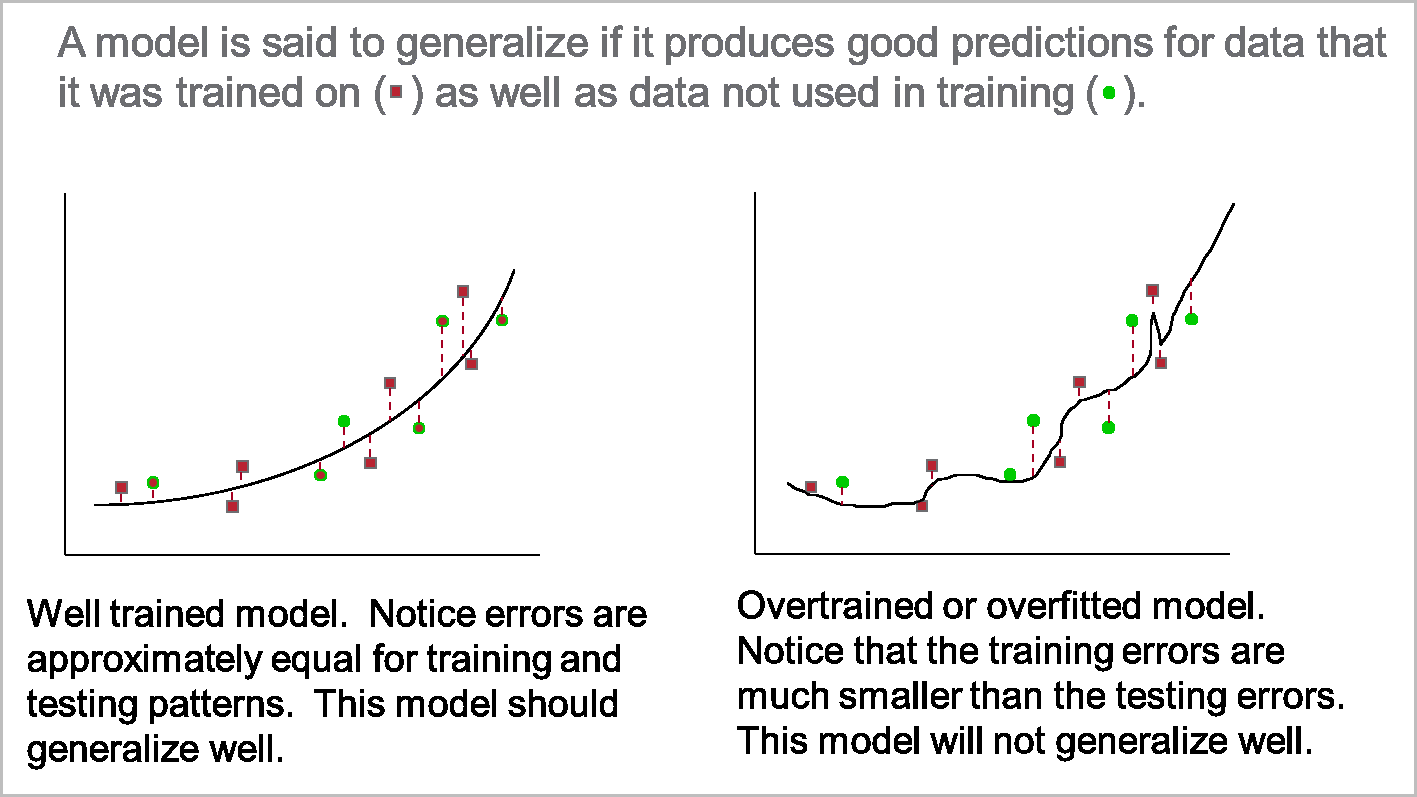
The intent and value of developing a run-time application is so that it represents well data that is not currently available as it will need to run and provide accurate predictions in the future. This is the primary driver for generalization as it also supports increased confidence that the model accurately represents the system, not just the available training data. Try not to overtrain models.
It is also important to note that any ML is driven by correlation with the output data but use the correlation analysis tools to make sure that input variables do not have strong (generally greater than 0.85) correlations. Anytime two input variables are strongly correlated and also similarly correlated with the output data the relative sensitivities can be anything and generally lose importance or causal information. I.e., consider a case where:
- Output = Input1 + 2* Input2
- But also, that Input1 = 2*Input2 (100% correlated)
- In that case, all the below and more solve this modeling objective:
- Output = 0* Input1 + 4* Input2
- Output = 2* Input1 + 0* Input2
- Output = 5* Input1 - 8* Input2
- Output = -2*Input1 + 8* Input2
Its best practice to eliminate correlated inputs and a variety of data preparation options can support what best reflects the data. We recommend that the data setup best match to the physical relationships and knowledge of the interaction of that data on the output. The user with measurement and system understanding should be the best judge even in the case that correlations are independent of the model target (for example, ratio controllers will force correlations such as these). Options include:
- Add Input1 & Input2, these are parallel measurements that should be summed.
- Average Input1 & Input2 when both have good quality, these are independent measurements of the same thing.
- Remove one of these two inputs because, while similar one fundamentally or physically has a more important relationship on the model output (for example, PID control loop PV/feedback, Setpoint or CV/output).
- Retail both inputs, but retain the primary input as is, and create a differentiated, more unique second input such as the normalized difference or ratio on the secondary input. This supports the use case where these are independent influences, that are frequently, but not always correlated to attempt to better learn the independent influences.
- Create a dependent variable model on a state measurement that changes from an independent input and use the independent input and model residual as output model inputs.Hybrid RANN Regression
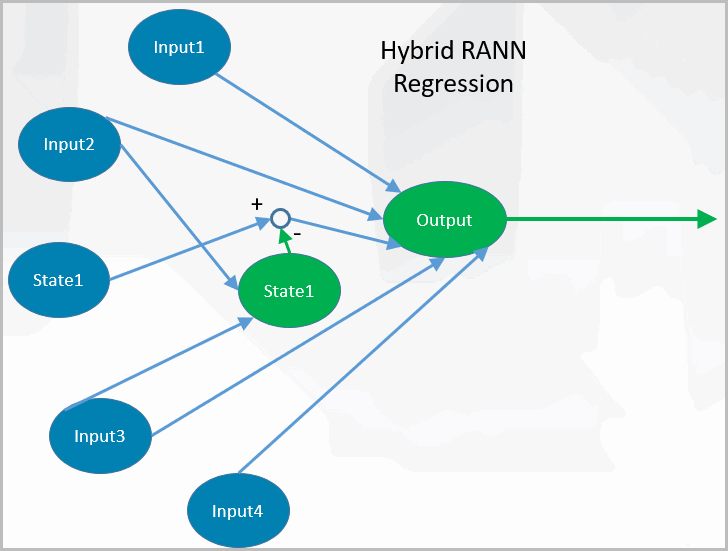
Use of Residual Activation Neural Network on dependent input variables.
Note that the challenges of correlated inputs tend to be much more significant on empirical modeling than physics-based modeling as with physics-based models (for example, implemented with expression modeling).
Best practice for modeling is supported within the Data Explorer workflow including:
- Reducing unnecessary model inputs
- Eliminating inappropriate or problematic measurement values or timeframes
- Deal with input measurement noise or dynamics with available filtering or transforms
- Eliminating or dealing with correlated model inputs
- Confirm data balance and consider corrections leveraging histogram plots on input variables.
Provide Feedback
